37%の法則とは?
皆さんは確率の話に興味はありますでしょうか?
私は大好きで、一時期は確率について調べ回っていました。その時にふと思った事を取り上げていきたいと思います。
”37%”という確率にまつわる数学的な話です。
秘書問題について
まず”秘書問題”と呼ばれている問題を取り上げてみます。
例えばあなたが社長となり、100人の秘書希望者と面接を行う事になったとしましょう。
- 1番~100番まで順番に面接を行い、その場で採用・不採用を告げていきます。
- 採用できるのはたった1人です。
- 1度不採用にした人はもう採用し直す事はできません
- 採用した後に残っている応募者に関しては顔を見る事もできません。
どんな人物が来るのか全く情報はありません。全員優秀かもしれないし、全員無能かもしれない。
そんな条件の中で出来るだけ優秀な人物を採用するためには、どのような進め方を行えば良いでしょうか?

計算上は以下の方法で進めるのが最適解となります。
- まず1番~37番までは全て不採用とします。
- その時に1番~37番の中で最も優秀だった人物を基準値として覚えておきます。
- 次に38番~100番まで順番に面接を行っていき、基準値となった人物より優秀な人物が現れたら即採用します。
この流れが優秀な人物を採用できる最も確率の高い方法とされています。
その基準として使用されるのが”37%”という確率になります。
今回は分かりやすく100人としただけで、応募者が1000人だろうと、1億人だろうと同じ確率になります。
※ちなみに厳密に行う場合は、50%まで行ったら今までで2番目以上に優秀であれば採用等、判定の基準は徐々に緩くなっていきますがここでは割愛します。
カードが一致する確率
AさんとBさんがそれぞれカードを持っているとします。
- Aさん(1・2・3)の3枚
- Bさん(1・2・3)の3枚
お互い無造作にカードを1枚ずつ同時に出します。
3枚のカードを出し終わるまでに、お互いのカードの値が1枚も一致しない確率はどれぐらいでしょう?

正解は”33%”です。
Aさんが1・2・3の順番で出したとして、Bさんの出し方は全6パターンあり、その中で(2・3・1)と(3・1・2)のみ一致しません。
つまり、2パターン/全6パターン=”33%”になるわけです。
「あれ、この流れは37%じゃないの?」と思うかもしれません。では、次にカードが4枚に増えたらどうなるのかを考えてみましょう。
この場合は、9パターン/全24パターン=”37%”になります。
出ました、あの確率です。
これだけでは「カード増やしたらどんどん確率が高くなるんじゃないの?」と思われる方もいるかもしれません。
しかし驚くべきは、カードを10枚に増やそうが、100枚、1億枚、1兆枚に増やそうが、計算上全て”37%”に収束するのです。
ドロップ率1%の罠
ドロップ率が1%のアイテムがあったとします。オンラインゲームの低確率レアアイテムがそんな確率だったりしますよね。
このドロップ率1%のアイテムですが、100体倒したからって100%獲得出来るわけではないですよね?複数獲得する人もいれば1つも獲得出来ない人もいます。
では、敵を100体倒した場合に、1つも獲得出来ない確率は何%だと思いますか?
そうです。正解は”37%”です。
100人いたら63人は獲得出来ますが、37人は獲得出来ないのです。
そして1/1万を1万回でも、1/1億を1億回でも”37%”に収束します。
プロスペクト理論による37%
株などの投資をやっている方は聞いた事がある理論かもしれません。
”プロスペクト理論”とは、特定の状況下で人がどのような確率を選択するかという心理学理論です。
理論の中では人間は利益を得る場面ではリスク回避を優先し、損失を被る場面ではリスク愛好(損失回避)を優先すると言われています。
例えば以下のような二択があったとします。
- 100%の確率で100万円が手に入る
- 50%の確率で200万円が手に入る、50%の確率で0円が手に入る
この場合、ほとんどの人は「1」を選択します。
どちらも期待値は100万円ですが、利益を得る場面のためリスク回避が先行するのです。
反対に
- 100%の確率で100万円を支払う
- 50%の確率で1円も支払わない、50%の確率で200万円を支払う
この場合は損失回避の思考になり、「2」を選ぶ人の方が多くなるのです。
そのプロスペクト理論の中で人間の体感する主観確率と、実際の客観確率との違いを述べています。
以下の”確率加重関数”というグラフを見てみてください。
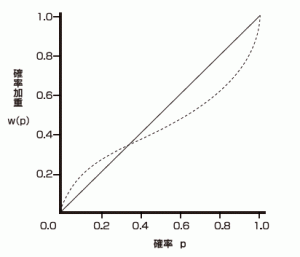
点線が主観確率、実線が客観確率になります。
主観確率の点線を見てみると確率の低い事象は過大評価し、確率の高い事象は過小評価する傾向にあります。「10%⇒20%」に感じてしまったり、「90%⇒70%」に感じてしまうのです。
そして主観確率と客観確率が重なる基準点をよく見てみてください。
そう、”37%”です。
人間は37%以下は過大評価、37%以上は過小評価して確率を判断してしまうのです。
ゲーム開発をしていれば大抵の場合は確率というものに触れると思います。
確率を扱う場合、この理論は非常に重要になるので是非覚えておいてください。
例えば鍛冶屋で精錬した時の成功確率を90%に設定したとします。ユーザー側の体感からしたら「90%だと?70~80%だろ!ウソつくな!」と言われてしまうのです。
それだったらいっそのこと70%ぐらいに設定した方が確率が体感に近づくため、失敗した時に「まぁ70%だし、しょうがないか」と思ってもらえたりするのです。
10%ぐらいの確率が20%ぐらいの確率に感じられるのも忘れてはいけません。
10%の確率で精錬効果が2倍になる、と設定しておけば、実際はそれほど起こっていなかったとしても「20%ぐらいの確率で起こってね?俺ラッキー!」となる可能性があるのです。
誕生日問題
他にも主観確率と客観確率がかけはなれている例を1つ挙げてみます。
突然ですがクラス40人いたとして同じ誕生日の生徒が1組以上存在する確率はどれぐらいだと思いますか?
- 10%
- 50%
- 90%
「1」の10%を選んだ方はおそらく自分を基準に、自分と同じ誕生日が残り39人の中にいる確率を求めてしまっていませんか?
「2」の50%を選んだ方は体感でこれぐらいかな?と思ったのかもしれません。
「3」の90%、実はこれが正解です。
知らない方にとっては「え?高すぎない?」と驚くかもしれません。
計算式的には1-(364/365×363/365×362/365・・・・×365-n+1/365)…
・・・分かりづらいのでざっくり解説します。
1人、2人、、、10人ぐらいまでは一致する確率は少ないので一旦スルーします。20人目になると今までの1~19人の誕生日と一致する確率なので既に5%ぐらいになっています。36人目なんて約10%の確率で一致します。
一回一回は低確率とは言え、40回の試行を重ねれば、かなりの確率で同じ誕生日のペアが見つかる気がしてきますよね。
参考までに同じ誕生日がいる確率が50%を超えるのは23人、99.9%を超えるのは70人となります。
最後に
大好物の話だったので長々書いてしまいました。
ちなみに野球の歴代最高打率は”37~38%”です。あれだけランダム性のあるゲームなのに最高値が収束しているのです。イチローですら39%の壁に届いていません。
また”37%”というのは”1”を数学者レオンハルト・オイラー氏が発見したネイピア数(2.71828…)という数学定数で割った値でもあります。
単なる偶然なのか、神が造りし確率なのかは知る由もありません。
ゲームでも重要な役割を持つ確率。
そこに目を向けてみると面白い発見があるかもしれません。
もしかしたら日常に潜む思わぬ確率が”37%”に収束しているかもしれませんね?











コメント